In den letzten Jahrzehnten ist eine neue interdisziplinäre Wissenschaft mit der Erforschung Komplexer Systeme entstanden (Simulation of Complex Adaptive Systems CAS). Die Wissenschaftsbereiche, in denen die Auseinandersetzung mit Komplexität und den damit verbundenen Eigenschaften Anwendung finden, sind äußerst vielfältig. Gemeinsam haben diese unterschiedlichen Forschungsfelder die Suche nach universellen Gesetzen und beobachtbaren Phänomenen und im Bereich der Komplexen Systeme die Ergründung der Relationen zwischen den einzelnen Elementen eines Ganzen. Die Erforschung von Komplexität gibt oft einen intuitiven Eindruck von Prinzipien und kann helfen, bestimmte Abläufe besser einzuschätzen.
Unternimmt man den Versuch, ein komplexes System zu beschreiben, treten allgemein ähnliche Charakteristika auf, die sich messen oder beschreiben lassen. Die zentrale Problemstellung der Komplexitätsforschung setzt sich nach der Erhebung von bestimmten Parametern mit Möglichkeiten und Wahrscheinlichkeiten auseinander.
Zuerst einmal geht es um die Feststellung folgender Parameter:
• Anzahl und Beschaffenheit vorhandener Elemente
• Art und Stärke der Interaktionen
• Formationsänderungen in der Zeit
• Vielfalt und Adaptionsfähigkeit
• Einfluss der Umgebung / des Umweltsystems
• Aktivität und Zielvorgabe
War man die der Lage diese Parameter zu definieren, so versucht man, Regeln (Algorithmen) zu (er)finden, mit deren wiederholter Anwendung sich ein Bild davon darstellen lässt, wie sich zukünftige Pfade entwickeln könnten.
Einfache, lineare Regeln führen mittels Iteration (Wiederholung) zu grafisch darstellbaren Verhältnissen, die in einem Zeitdiagramm exponentielles Wachstum von Faktoren erkennen lassen. Die folgenden Abbildungen zeigen drei unterschiedliche exponentielle Kurven, die mittels Wachstumsfaktor r, Anfangspopulation N(0) eine Populationsentwicklung entlang der Zeitlinie t darstellen.
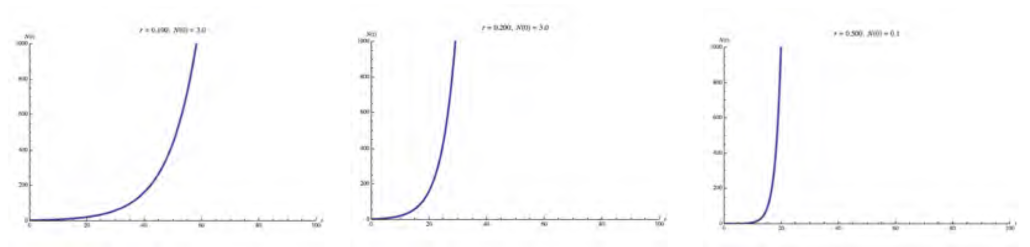
Anfangspopulation N(0) = 10 AnfangspopulationN(0) = 3 AnfangspopulationN(0) = 1
Die Unterschiede in diesen drei Kurven sind abhängig von der Größe der Anfangspopulation und der Annahme eines Wachstumsfaktors, woraus sich die Veränderungen in der Zeit ergeben. Unterschiedliche Einstellung der einzelnen Parameter führt damit zu unterschiedlichen Ergebnissen unter Berücksichtigung der verbrauchten Zeit. Das Prinzip des Ablaufs ist dabei jedoch nicht durch eine quantitative Definition bestimmt, sondern durch den prinzipiell qualitativen Algorithmus.
Bekannt wurde dieses Prinzip mit den Untersuchungen des Meteorologen Edward Lorenz, der im Zuge von computergestützten Berechnungen zur Wettervorhersage mittels Differentialgleichungen feststellte, dass geringfügig unterschiedliche Anfangsbedingungen im Laufe der Zeit durch Selbstverstärkung enorme Auswirkungen zeitigen können. Dies wurde in der Folge als Schmetterlingseffekt bezeichnet. (Link zum Paper Deterministic Nonperiodic Flow – 1963)
Die Einschränkung dieser speziellen Wachstumsdarstellung auf ausschließlich drei Faktoren ist eine reduktionistisch motivierte Vereinfachung. Besonders die Annahme eines Wachstumsfaktors verlangt, dass dieser Faktor unter Bedingungen natürlicher Umgebung einer laufenden Veränderung unterworfen ist, die selbst wieder als komplex beschrieben werden kann.
Dazu folgende Hinweise:
In natürlicher Umgebung werden voraussichtlich wesentlich mehr als drei Faktoren eine Rolle spielen, d. h. es wird mit positivem oder negativem Feedback zu rechnen sein, was für Interaktionen mit einem oder mehreren sich verändernden Umweltfaktoren spricht.
Die Einschätzung einer zukünftigen Entwicklung ist abhängig vom Blickwinkel derer, die diese Beobachtungen tätigen. Dies bedeutet, dass aus Sicht unterschiedlicher Wissenschaften unterschiedliche Modellrechnungen angestellt werden können, dabei jedoch jedenfalls das Prinzip der Exponentialität gleich bleibt. In der allgemeinen Lebenswelt spricht man dabei von Voraussetzungen, im wissenschaftlichen Umfeld von Axiomen, in der Auseinandersetzung mit der Natur von Naturgesetzen.


